|
l |
e |
u |
w |
g |
|
r |
x |
d |
s |
o |
|
m |
h |
b |
z |
t |
|
y |
p |
0 |
a |
c |
|
% |
n |
j |
i |
Рис. 6. Полибианский квадрат, заполненный случайным образом 24 буквами греческого алфавита и пробелом
При шифровании в этом полибианском квадрате находили очередную букву открытого текста и записывали в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывалась в нижней строке таблицы, то для шифртекста брали самую верхнюю букву из того же столбца. Например, для слова
t
a u r o sполучается шифртекст
Х
j d m t xКонцепция полибианского квадрата оказалась плодотворной и нашла применение в криптосистемах последующего времени.
Система шифрования Цезаря
Шифр Цезаря является частным случаем шифра простой замены (одноалфавитной подстановки). Свое название этот шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке с Цицероном (около 50 г. до н.э.).
При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на К букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал шифр замены при смещении К = 3. Такой шифр замены можно задать таблицей подстановок, содержащей соответствующие пары букв открытого текста и шифртекста. Совокупность возможных подстановок для К = 3 показана в табл. 3.
Таблица 3 Одноалфавитные подстановки (К = 3, m = 26)
|
A ® D |
J ® M |
S ® V |
|
B ® E |
K ® N |
T ® W |
|
С ® F |
L ® O |
U ® X |
|
D ® G |
M ® P |
V ® Y |
|
Е ® H |
N ® Q |
W ® Z |
|
F ® I |
O ® R |
X ® A |
|
G ® J |
P ® S |
Y ® B |
|
Н ® K |
Q ® T |
Z ® C |
|
I ® L |
R ® U |
|
Например, послание Цезаря
VENI VIDI VICI
в переводе на русский означает "Пришел, Увидел, Победил"), направленное его другу Аминтию после победы над понтийским царем Фарнаком, сыном Митридата,
выглядело бы в зашифрованном виде так:YHQL YLGL YLFL
Выполним математический анализ шифра простой замены (подстановки) на основе понятий, введенных в начале главы.
Подстановка в алфавите ![]() является взаимно однозначным отображением
является взаимно однозначным отображением
p
: t ® p(t),которое заменяет букву t открытого текста на букву
p(t) шифртекста. Множество всех подстановок на1.
Замкнутость. Произведение подстановок p1p2 является подстановкой:![]()
p
: t ® p1(p2 (t)).2.Ассоциативность. Оба способа заключения в скобки произведения подстановок p1p2p3:
p1(p2p3) = (p1p2)p3
дают одинаковый результат.
3.
Существование единичного элемента. Подстановка d, определенная какd
(t) = t, 0 Ј t < m,является единственным единичным элементом группы ![]() по умножению
по умножению
dp
=dp для всех4.
Существование обратных элементов. Для каждой подстановки p имеется взаимно однозначно определенная обратная подстановка, обозначаемая p-1, которая удовлетворяет соотношению:p p-
1 = d.Указанные свойства являются аксиомами группы. Ключ К подстановки для алфавита ![]() представляет собой последовательность элементов симметричной группы из
представляет собой последовательность элементов симметричной группы из ![]()
К=(
p0, p1, ..., pn-1, ...),Подстановка, определяемая ключом
К, является криптографическим преобразованием ЕК, которое шифрует n-грамму(x0, x1, x2, ..., xn-1)
открытого текста в n-грамму
(y0, y1, y2, ..., yn-1)
шифртекста, где
y i =
pi ( xi), 0 Ј i < n,для каждого n, n = 1, 2, 3, ... .
Криптографическое преобразование Ек называется одно-алфавитной подстановкой, если значение
pi одинаково для каждого i, i = 0,1,2,...; в противном случае преобразование Ек называется многоалфавитной подстановкой.На рис.7 представлена схема реализации подстановки Ек.
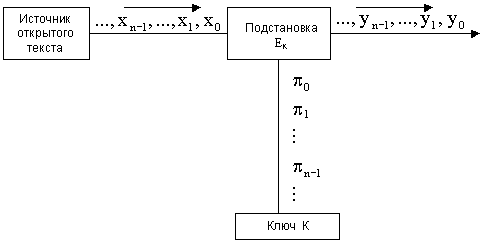
Рис. 7. Схема подстановки Ек
Отметим характерные особенности подстановки ЕК
:• открытый текст шифруется побуквенно (буква за буквой);
• i-я буква y
i шифртекста является функцией только i-й компоненты pi ключа К и i-й буквы хi открытого текста;• шифрование n-граммы (x
0,x1,x2,...,xn-1) производится в соответствии с формулой(y0,y1,y2,...,yn-1) =
ЕК (x 0,x 1,x2,...,xn-1)Система Цезаря представляет собой одноалфавитную подстановку, которая шифрует n-грамму (x
0,x1,x2,...,xn-1) открытого текста в n-грамму (y0,y1,y2,...,yn-1) шифртекста согласно следующему правилу:y i
= ЕК (хi), 0 Ј i < n, (3)ЕК
: j ® (j + К) (mod n), 0 Ј К < m,где j - числовой код буквы открытого текста; j + К - числовой код соответствующей буквы шифртекста.
В отличие от шифра Цезаря, описанного в начале этого подраздела, система шифрования Цезаря образует по существу семейство одноалфавитных подстановок для выбираемых значений ключа К, причем
0 Ј К < m.Достоинством системы шифрования Цезаря является простота шифрования и расшифрования. К недостаткам системы Цезаря следует отнести следующие:
• подстановки, выполняемые в соответствии с системой Цезаря, не маскируют частот появления различных букв исходного открытого текста;
• сохраняется алфавитный порядок в последовательности заменяющих букв; при изменении значения К изменяются только начальные позиции такой последовательности;
• число возможных ключей К мало;
• шифр Цезаря легко вскрывается на основе анализа частот появления букв в шифртексте.
Криптоаналитическая атака против системы одноалфавитной замены начинается с подсчета частот появления символов: определяется число появлений каждой буквы в шифртексте. Затем полученное распределение частот букв в шифртексте сравнивается с распределением частот букв в алфавите исходных сообщений, например в английском. Буква с наивысшей частотой появления в шифртексте заменяется на букву с наивысшей частотой появления в английском языке и т.д. Вероятность успешного вскрытия
системы шифрования повышается с увеличением длины шифртекста.Концепция, заложенная в систему шифрования Цезаря, оказалась весьма плодотворной, о чем свидетельствуют ее многочисленные модификации. Несколько таких модификаций будут рассмотрены ниже.
Аффинная система подстановок Цезаря
В системе шифрования Цезаря использовались только аддитивные свойства множества целых ![]() . Однако символы множества
. Однако символы множества ![]() можно также умножать по модулю m. Применяя одновременно операции сложения и умножения по модулю m над элементами множества
можно также умножать по модулю m. Применяя одновременно операции сложения и умножения по модулю m над элементами множества ![]() , можно получить систему подстановок, которую называют аффинной системой подстановок Цезаря.
, можно получить систему подстановок, которую называют аффинной системой подстановок Цезаря.
Определим преобразование в такой системе:
![]()
![]()
![]() (4)
(4)
где а,b - целые числа, ![]()
В данном преобразовании буква, соответствующая числу t, заменяется на букву, соответствующую числовому значению (at+b) по модулю m.
Следует заметить, что преобразование E
a,b(t) является взаимно однозначным отображением на множестве Zm только в том случае, если наибольший общий делитель чисел а и m, обозначаемый как НОД(а,m), равен единице, т.е. а и m должны быть взаимно простыми числами.Например, пусть m=26, а=3, b=5. Тогда, очевидно, НОД (3,26)=1, и мы получаем следующее соответствие между числовыми кодами букв:
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
3t+5 |
5 |
8 |
11 |
14 |
17 |
20 |
23 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
2 |
Преобразуя числа в буквы английского языка, получаем следующее соответствие для букв открытого текста и шифртекста:
|
А |
B |
C |
D |
Е |
F |
Q |
Н |
I |
J |
К |
L |
М |
N |
0 |
Р |
Q |
R |
S |
T |
U |
V |
W |
Х |
Y |
Z |
|
F |
I |
L |
O |
R |
U |
Х |
А |
D |
Q |
J |
М |
Р |
S |
V |
Y |
В |
Е |
Н |
K |
N |
Q |
Т |
W |
Z |
C |
Исходное сообщение HOPE преобразуется в шифртекст AVYR
Достоинством аффинной системы является удобное управление ключами - ключи шифрования и расшифрования представляются в компактной форме в виде пары чисел (а, b). Недостатки аффинной системы аналогичны недостаткам системы шифрования Цезаря.
Аффинная система использовалась на практике несколько веков назад, а сегодня ее применение ограничивается большей частью иллюстрациями основных криптологических положений.
Система Цезаря с ключевым словом
Система шифрования Цезаря с ключевым словом является одноалфавитной системой подстановки. Особенностью этой системы является использование ключевого слова для смещения и изменения порядка символов в алфавите подстановки.
Выберем некоторое число k, ![]()
Ключевое слово записывается под буквами алфавита, начиная с буквы, числовой код которой совпадает с выбранным числом k:
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
10 |
|
|
|
|
15 |
|
|
|
|
20 |
|
|
|
|
25 |
|
А |
B |
C |
D |
Е |
F |
Q |
Н |
I |
J |
К |
L |
М |
N |
0 |
Р |
Q |
R |
S |
T |
U |
V |
W |
Х |
Y |
Z |
|
|
|
|
|
|
D |
I |
P |
L |
O |
M |
A |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
Оставшиеся буквы алфавита подстановки записываются после ключевого слова в алфавитном порядке:
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
B |
C |
D |
Е |
F |
Q |
Н |
I |
J |
К |
L |
М |
N |
0 |
Р |
Q |
R |
S |
T |
U |
V |
W |
Х |
Y |
Z |
|
V |
W |
Х |
Y |
Z |
D |
I |
P |
L |
O |
M |
A |
T |
B |
C |
E |
F |
G |
H |
J |
K |
N |
Q |
R |
S |
U |
Теперь мы имеем подстановку для каждой буквы произвольного сообщения.
Исходное сообщение SEND MORE MONEY шифруется как HZBY TCGZ TCBZS
Следует отметить, что требование о различии всех букв ключевого слова не обязательно. Можно просто записать ключевое слово (или фразу) без повторения одинаковых букв. Например, ключевая фраза
КАК ДЫМ ОТЕЧЕСТВА НАМ СЛАДОК И ПРИЯТЕН
и число k=3 порождают следующую таблицу подстановок:
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
Й |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Ъ |
Э |
Ю |
Я |
|
Ъ |
Э |
Ю |
К |
А |
Д |
Ы |
М |
О |
Т |
Е |
Ч |
С |
В |
Н |
Л |
И |
П |
Р |
Я |
Б |
Г |
Ж |
З |
Й |
У |
Ф |
Х |
Ц |
Ш |
Щ |
Ь |
Несомненным достоинством системы Цезаря с ключевым словом является то, что количество возможных ключевых слов практически неисчерпаемо. Недостатком этой системы является возможность взлома шифртекста на основе анализа частот появления букв.
Шифрующие таблицы Трисемуса
В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием "Полиграфия". В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку.
Поскольку ключевое слово или фразу легко хранить в памяти, то такой подход упрощал процессы шифрования и расшифрования. Поясним этот метод шифрования на примере. Для русского алфавита шифрующая таблица может иметь размер 4х8. Выберем в качестве ключа слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом показана на рис. 8.
|
Б |
А |
Н |
Д |
Е |
Р |
О |
Л |
|
Ь |
В |
Г |
Ж |
3 |
И |
Й |
К |
|
М |
П |
С |
Т |
У |
Ф |
Х |
Ц |
|
Ч |
Ш |
Щ |
Ы |
Ъ |
Э |
Ю |
Я |
Рис. 8. Шифрующая таблица с ключевым словом БАНДЕРОЛЬ
Как и в случае полибианского квадрата, при шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю букву из того же столбца.
Например, при шифровании с помощью этой таблицы сообщения
ВЫЛЕТАЕМПЯТОГО
получаем шифртекст
ПДКЗЫВЗЧШЛЫЙСЙ
Такие табличные шифры называются монограммными, так как шифрование выполняется по одной букве. Трисемус первым заметил, что шифрующие таблицы позволяют шифровать сразу по две буквы. Такие шифры называются биграммными.
Биграммный шифр Плейфейра
Шифр Плейфейра, изобретенный в 1854 г., является наиболее известным биграммным шифром замены. Он применялся Великобританией во время первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.
Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущего раздела (см. рис 8).
Процедура шифрования включает следующие шаги:
1. Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
2. Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а. Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.8), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это буквы АЙОВ. Пара букв АЙ отображается в пару 0В. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста).
2б. Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в. Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.).
Зашифруем текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Разбиение этого текста на биграммы дает
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы (см. рис.8) в следующую последовательность биграмм шифртекста
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
При расшифровании применяется обратный порядок действий.
Следует отметить, что шифрование биграммами резко повышает стойкость шифров к вскрытию. Хотя книга И.Трисемуса "Полиграфия" была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.
Криптосистема Хилла
Алгебраический метод, обобщающий аффинную подстановку Цезаря
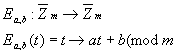
для определения n-грамм, был сформулирован Лестером С.Хиллом.
Множество целых ![]() , для которого определены операции сложения, вычитания и умножения по модулю m, является примером кольца. Кольцо R представляет собой алгебраическую систему, в которой определены операции сложения, вычитания и умножения пар элементов. Эта алгебраическая система обладает рядом свойств:
, для которого определены операции сложения, вычитания и умножения по модулю m, является примером кольца. Кольцо R представляет собой алгебраическую систему, в которой определены операции сложения, вычитания и умножения пар элементов. Эта алгебраическая система обладает рядом свойств:
• элементы кольца R образуют коммутативную группу относительно операции сложения; кроме того, существуют единичный и обратный элементы относительно операции сложения;
• умножение и сложение удовлетворяют ассоциативному и дистрибутивному законам.
Мультипликативное обратное
a-1 элемента a кольца может существовать не всегда. Например, если модуль m = 26, то значения 2-1(mod 26) и 13-l(mod 26) не могут существовать.• Если модуль m является простым числом p, то существует обратная величина любого ненулевого элемента t из
t (mod m), 2t (mod m), 3t (mod m),.... (p-1) t (mod m)
различаются, если
1 Ј t Ј p-1.Множество
Множество всех n-грамм
![]() ,
,
если
![]() (5)
(5)
Линейное преобразование
![]() ,
,
![]() , (6)
, (6)
которое удовлетворяет условию линейности
![]()
для всех s, t в
Линейное преобразование
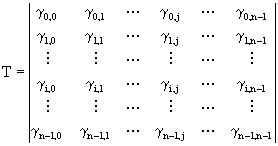 , (7)
, (7)
причем
![]()
или
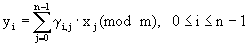
Базисом для векторного пространства
Пуст
ь![]() .
.
Если векторы
![]() ,
,
![]() , (8)
, (8)
где
Например, когда m=26 и матрица преобразования
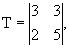
то определитель этой матрицы
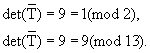
Поэтому существует обратное преобразование
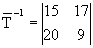
удовлетворяет соотношению
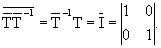
Пусть
![]()
Используем это преобразование ![]() для определения биграммной подстановки в английском алфавите {ABCDEFGH…XYZ}.
для определения биграммной подстановки в английском алфавите {ABCDEFGH…XYZ}.
Сначала разобьем n-грамму открытого текста на биграммы, причем выберем n кратным 2, например, 12-грамма PAYMOREMONEY делится на шесть биграмм:
PA YM OR ЕМ ON EY
Затем в каждой биграмме открытого текста заменим каждую букву ее числовым эквивалентом из таблицы:
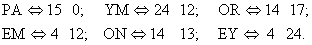
Преобразование биграмм
![]()
или
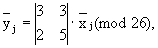
где
Получаем
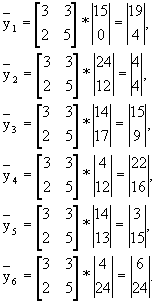
Заменяя в биграммах шифртекста числа на соответствующие буквы согласно табл.2.2, получаем 12-грамму шифртекста:
ТЕ ЕЕ
PJ WQ DP GYДля расшифрования биграмм
Система Хилла является одноалфавитной в широком смысле слова.
Система омофонов
Система омофонов обеспечивает простейшую защиту от криптоаналитических атак, основанных на подсчете частот появления букв в шифртексте. Система омофонов является одноалфавитной, хотя при этом буквы исходного сообщения имеют несколько замен. Число замен берется пропорциональным вероятности появления буквы в открытом тексте.
Данные о распределениях вероятностей букв в русском и английском текстах приведены в табл.4 и 5. Буквы в таблицах указаны в порядке убывания вероятности их появления в тексте. Например, русская буква Е встречается в 36 раз чаще, чем буква Ф, а английская буква Е встречается в 123 раза чаще, чем буква Z.
Шифруя букву исходного сообщения, выбирают случайным образом одну из ее замен. Замены (часто называемые омофонами) могут быть представлены трехразрядными числами от 000 до 999. Например, в английском алфавите букве Е присваиваются 123 случайных номера, буквам В и G - по 16 номеров, а буквам J и Z - по 1 номеру. Если омофоны (замены) присваиваются случайным образом различным появлениям одной и той же буквы, тогда каждый омофон появляется в шифртексте равновероятно.
Таблица 4. Распределение вероятностей букв в русских текстах
|
Буква |
Вероятность |
Буква |
Вероятность |
Буква |
Вероятность |
Буква |
Вероятность |
|
Пробел |
0,175 |
Р |
0,040 |
Я |
0,018 |
X |
0,009 |
|
О |
0,090 |
В |
0,038 |
Ы |
0.016 |
Ж |
0,007 |
|
Е |
0,072 |
Л |
0,035 |
3 |
0,016 |
Ю |
0,006 |
|
А |
0,062 |
K |
0,028 |
Ъ |
0,014 |
Ш |
0,006 |
|
И |
0,062 |
M |
0,026 |
Б |
0,014 |
Ц |
0,004 |
|
Н |
0,053 |
Д |
0,025 |
Г |
0,013 |
Щ |
0,003 |
|
Т |
0,053 |
П |
0,023 |
Ч |
0,012 |
Э |
0,003 |
|
C |
0,045 |
У |
0,021 |
Й |
0,010 |
Ф |
0,002 |
Таблица 5. Распределение вероятностей букв в английских текстах
|
Буква |
Вероятность |
Буква |
Вероятность |
Буква |
Вероятность |
|
Е |
0,123 |
L |
0,040 |
В |
0,016 |
|
Т |
0,096 |
D |
0,036 |
G |
0,016 |
|
А |
0,081 |
С |
0,032 |
V |
0,009 |
|
O |
0,079 |
U |
0,031 |
К |
0,005 |
|
N |
0,072 |
Р |
0,023 |
Q |
0,002 |
|
I |
0,071 |
F |
0,023 |
X |
0,002 |
|
S |
0,066 |
М |
0,022 |
J |
0,001 |
|
R |
0,060 |
W |
0,020 |
Z |
0,001 |
|
Н |
0,051 |
Y |
0,019 |
|
|
При таком подходе к формированию шифртекста простой подсчет частот уже ничего не дает криптоаналитику. Однако в принципе полезна также информация о распределении пар и троек букв в различных естественных языках. Если эту информацию использовать при криптоанализе, он будет проведен более успешно.